Transformation naturelle
En théorie des catégories, une transformation naturelle permet de transformer un foncteur en un autre tout en respectant la structure interne (c'est-à-dire la composition des morphismes) des catégories considérées. On peut ainsi la voir comme un morphisme de foncteurs.
Définition
[modifier | modifier le code]Soient et deux catégories, F et G deux foncteurs covariants de dans . Une transformation naturelle η de F vers G est la donnée, pour tout objet X de , d'un morphisme de :
tel que pour tous objets X et Y de et tout morphisme de X dans Y, le diagramme suivant soit commutatif :
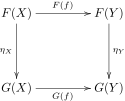
c'est-à-dire tel que :
On peut de même définir la notion de transformation naturelle entre deux foncteurs contravariants en inversant uniquement le sens des flèches horizontales du diagramme ci-dessus.
Si pour tout objet X de , ηX est un isomorphisme, on dit que η est une « équivalence naturelle » ou un « isomorphisme naturel ».
Bibliographie
[modifier | modifier le code](en) Saunders Mac Lane, Categories for the Working Mathematician [détail de l’édition]





